Archive for 2014
PYTHAGOREAN THEOREM EXPLORATION 2 (CUT-OUTS)
 |
| Pythagorean Theorem Exploration 2 Cutouts |
You may download this template for personal use and for your math class activity. The length of the sides on the second page measures 6.5 inches. This is also the measure of the length of the hypotenuse of the right triangle on the first page.
Your comments and suggestions are welcome here. Write them in the comment box below.
Don't forget to like and share.... :)
Thank you and God bless!
Don't forget to like and share.... :)
Thank you and God bless!
Friday, November 21, 2014
PYTHAGOREAN THEOREM EXPLORATION 1 (CUT-OUTS)
 |
| Pythagoras Theorem Cutouts |
The Pythagoras Theorem states that:
"The square of the length of the hypotenuse (denoted by c) is equal to the sum of the squares of the lengths of the other two sides (denoted by a and b)"
 |
| Pythagoras Theorem |
Here is the cutout for the first exploration of the Pythagoras Theorem. The file consist of two pages. The first page consists of four congruent right triangles. The second page is a square.
Cut along the broken lines on the right triangles and use them to fill in the square on the second page using the EXPLORATION 1 as a guide.
You comments and suggestions are welcome here. You may write them in the comment box below.
Monday, November 17, 2014
PYTHAGOREAN THEOREM (Exploration 2)
 |
| The Pythagorean Theorem |
Start with a cutout of a right triangle.
Cut three more cutouts.
Let us name the sides of the right triangle with c as the hypotenuse.
Now, let us form a square using the four (4) triangles. This time, use the hypotenuse as the sides of the square.
Let us take a look at the different parts of the square we formed. If we separate the whole square, we can get its area in terms of c.
The middle part is also a square with sides equal to the difference of sides b and a. The area can be obtained as
On the other hand, the area of the four triangles outlining the sides of the whole square is as follows.
Combining their areas, we obtain
Thus, c^2 = a^2 + b^2.
Your questions, comments and suggestions are welcome here. Kindly write them in the comment box below.
Sunday, August 17, 2014
PYTHAGOREAN THEOREM (Exploration 1)
 |
| The Pythagoras' Theorem |
The theorem states that the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the remaining sides. That is c^2 = a^2 + b^2, where c is the hypotenuse, a and b are the lengths of the remaining sides.
Here is one of the theorem. Take note that the theorem only applies to right triangles.
Start with a cutout of any right triangle.
Let us name the shortest side as a, the longer side as b and the hypotenuse as c.
Let us make three (3) more of the right triangle.
Our next step is to form a square out of the four (4) triangles, making sure that the combined length of a and b will be the length of the side of the square that we are forming.
Let us take a look at the different parts of the square we formed. If we separate the whole square, we can get its area in terms of a and b.
The middle part is also a square with sides equal to the hypotenuse of the right triangle. The area can also be obtained.
The area of the four right triangles outlining the sides of the whole square is as follows
We take note that the area of the whole square is equal to the area of the small square in the middle added to the area of the four right triangles. That is
Thus, c^2 = a^2 + b^2.
Hope this will help you understand the derivation of the Pythagoras' Theorem.
Your comments and suggestions are welcome here. You may write them in the comment box below. Thank you!
Saturday, May 24, 2014
Sunday, March 23, 2014
EXTERIOR ANGLE THEOREM (Part 1: Exploration)

On the other hand, how many are you are familiar with the exterior angle theorem? What is the relationship of the exterior angles with the interior angles? The answer for these questions can be summarized by the "Exterior Angle Theorem".
In this post, let us discover where this theorem come from by using some illustrative examples.
Materials needed: ruler, protractor, calculator and pencil
Procedure:
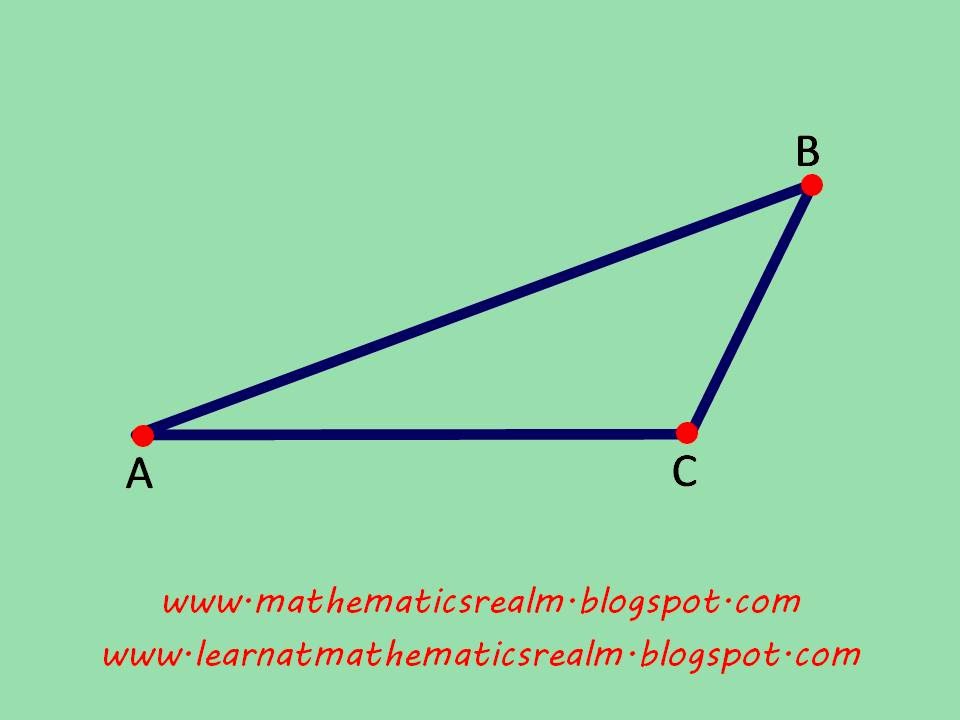
1) On a piece of paper, draw one (1)
acute triangle, one (1) right triangle, and one (1) obtuse triangle. Name each
triangle as triangle ABC, with AC as the base.
2) Extend the base of AC to a point
D. Points A, C and D should be on the same line and C is between A and D.
- angle BCD is the exterior angle of each triangle
- angles A and B are the remote (non-adjacent) interior angles of each triangle
4) Look at the rightmost part of the table. Compare the sum of the measures of angles A and B and the exterior angle.
5) We can now make a conclusion/generalization about the relationship of the measurement of the exterior angle and the remote interior angles.
Here is the pdf copy of the activity, if to be conducted in a classroom setting. You are free to download it and use for your class. Hope it will be beneficial for you.
Your comments and suggestions are accepted here. Just write them in the comment box below. Thank you!
Thursday, March 20, 2014