Learn at Mathematics Realm

Here is another proof of the Pythagorean theorem.
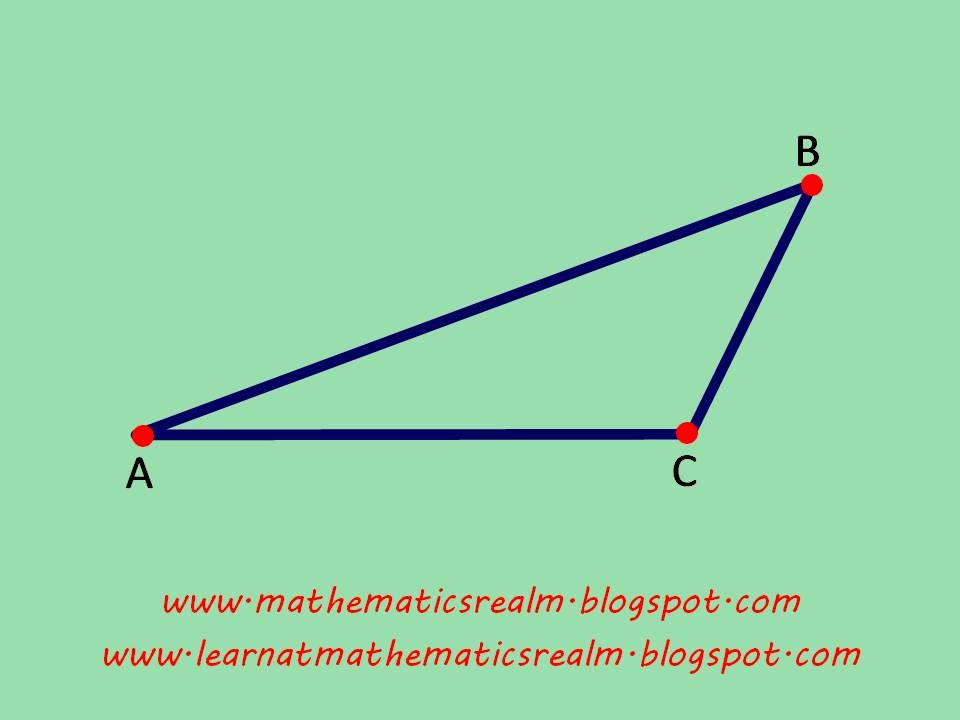
Let us use a right triangle and name the shortest side as a, the longer side as b, and the hypotenuse as c.
Let us make three more of these so we have four congruent right triangles.
Now, let us arrange the four right triangles to form a square like this
In this figure, there are two squares formed. The first square is larger square, with side equal to a+b, while the second square is the inner square with side equal to c.

Let us focus on the inner square. The length of its side is equal to the hypotenuse of the four right triangles. It means that it has sides each measuring as c. Hence, the area of the square is c^2. 
Let us take note of that the ares of the inner square is c^2.
Now, let us label the four right triangles as triangle 1, triangle 2, triangle 3 and triangle 4. This will make it easier for us to identify which triangle is moved later. 
Let us rearrange the triangles. Let us move triangle 2 beside triangle 1, and triangle 4 beside triangle 3. In this case, each pair will form a rectangle.
Let us focus on the area being left by the two triangles and shade it with white.
If you notice, the white area can be divided into two like this
We formed two quadrilaterals but we are not yet sure if they are squares or not. 

The smaller quadrilateral has a side that is equal to the shortest side of triangle 4. This means that this side measures a. 
On the other hand, if we slide back triangle 2, we could see that the upper side of the small quadrilateral is also the shortest side of triangle 2. 
This means that the upper side of the small quadrilateral measures a. Hence, the small quadrilateral is a square.
The area of the small square is
Now, let us look at the bigger quadrilateral shaded with white. One of its side (leftmost) has the same length as the longer side of triangle 2. It means that this side measures b.
On the other hand, if we slide back triangle 4, we could see that its longer side coincides with the lower side of the big white quadrilateral.
This means that the measure of the lower side of the big white quadrilateral is b. Hence, the big white quadrilateral is a square.
The area of the big white square is

If we compare the two figures formed. Both of them has four (4) right triangles and the areas of these triangles are the same. It means that the area of the white inner square in the first figure is the same as the area of the two white squares in the second figure.
Therefore, for any right triangles 

The Pythagoras' Theorem

The Pythagorean theorem is also known as the Pythagoras' theorem. It is named after a famous Greek mathematician, Pythagoras, who is credited for its proof.

The theorem states that the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the remaining sides. That is c^2 = a^2 + b^2, where c is the hypotenuse, a and b are the lengths of the remaining sides.

Here is one of the theorem. Take note that the theorem only applies to right triangles.
Start with a cutout of any right triangle.
 Let us name the shortest side as a, the longer side as b and the hypotenuse as c.
Let us make three (3) more of the right triangle.
Our next step is to form a square out of the four (4) triangles, making sure that the combined length of a and b will be the length of the side of the square that we are forming.


Let us take a look at the different parts of the square we formed. If we separate the whole square, we can get its area in terms of a and b.

The middle part is also a square with sides equal to the hypotenuse of the right triangle. The area can also be obtained.

The area of the four right triangles outlining the sides of the whole square is as follows

We take note that the area of the whole square is equal to the area of the small square in the middle added to the area of the four right triangles. That is
Thus, c^2 = a^2 + b^2.

Hope this will help you understand the derivation of the Pythagoras' Theorem.

Your comments and suggestions are welcome here. You may write them in the comment box below. Thank you!

Here is the two-column proof for the EXTERIOR ANGLE THEOREM. You may download and print it for your perusal.

Many are already familiar with the angles of a triangle. Many can easily point out which are the interior angles and even draw the exterior angles.

claimtoken-520b0b4c2af35