- Back to Home »
- 1 = 2?
Friday, June 21, 2013
Maybe you are wondering why or how can 1 be equal to 2. Let us look at the following proof:
If we simplify both sides by combining like terms, it will become
Now let us subtract 2a on both sides
The right side has a common factor, which is 2. Using distributive property, it can be rewritten as
If you notice, both sides has a common factor, which is b - a. To simplify the equation, let us divide both sides by the common factor.
The process will arrive at
Are you convinced? No no no...
Seems like the proof is valid but there is something wrong with it. Look over the proof once again. Can you identify which of the process is not valid?
There is nothing wrong with the given. Real numbers can be equal. There is nothing wrong also with adding b and subtracting 2a on both sides. Likewise, there is nothing wrong with combining like terms on both sides. Then, where is the mistake?
There is nothing wrong with dividing both sides by any number but in this case it becomes invalid. The reason is that b - a = 0 since a = b. Subtracting equal numbers will yield 0. Since b - a = 0, then the result will be UNDEFINED. We cannot also cancel out b - a on both sides because of that.
Therefore, 1 is not equal to 2.
Here is a copy of the proof in pdf form. You may download and print it for educational purposes. You may share it to your friends. Your comments and suggestions are also welcome here.






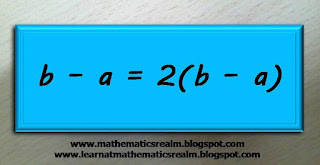




























Statement 2 is not valid.
ReplyDeleteWhy do you think statement 2 is not valid?
DeleteI think is the number 7; if a = b so, b - a is 0 division by cero is illegal.
DeleteSimplification on 0/0 which is an indetermination. Cheers from Spain!!! Great blog.
ReplyDeleteYes, 0/0 is indeterminate. Thank you for visiting here! Hope you could share it also to your friends...
DeleteGood information!
ReplyDelete